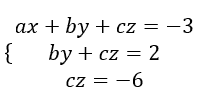Ingin mengasah pengetahuan materi SPLTV pada matematika? Coba saja isi contoh soal SPLTV ini!
Matematika merupakan salah satu mata pelajaran penting yang diajarkan di sekolah.
Salah satu materi yang sering dipelajari adalah Sistem Persamaan Linear Tiga Variabel (SPLTV).
Melansir dari repository.radenintan.ac.id, adapun SPLTV merupakan sistem persamaan yang memiliki tiga variabel berpangkat satu serta dihubungkan dengan tanda (=).
SPLTV melibatkan tiga variabel yang saling berkaitan dalam persamaan linear.
Menemukan solusi dari sistem ini bagaikan memecahkan teka-teki rumit, di mana kita harus memanipulasi persamaan dengan berbagai metode untuk menemukan nilai x, y, dan z yang memenuhi semua persamaan.
Nah, artikel ini akan menghadirkan contoh soal SPLTV yang dapat membantu kamu memahami konsep dan cara menyelesaikannya.
Yuk, lihat informasinya pada uraian di bawah ini!
5 Contoh Soal SPLTV Beserta Jawabannya
Sumber: freepik.com
Contoh Soal SPLTV 1
Diketahui persamaan bidang 𝐷 ≡ 3𝑥 + 4𝑦 − 𝑧 = Apakah titik-titik berikut terletak pada bidang D?
- (0, 4, 5)
- (1, 0, −9)
- (3, 1, −2)
- (4, 1, −4)
Pembahasan
Kita dapat menentukan apakah suatu titik terletak pada bidang dengan menyubstitusikan nilai koordinat x, y, dan z tersebut ke dalam persamaan bidang.. Jika menghasilkan pernyataan yang benar, titik tersebut terletak pada bidang
a. (0 ,4, 5)
3.0 + 4.4 − 5 = 12
0 + 16 − 5 = 12
11 = 12 pernyataan salah. Jadi, titik (0,4,5) tidak terletak pada bidang D
b. (1, 0, −9)
3.1 + 4.0 − (−9) = 12
– 3 + 0 + 9 = 12
12 = 12 pernyataan benar. Jadi, titik (1,0, −9) terletak pada bidang D
c. (3, 1, −2)
3.3 + 4.1 − (−2) = 12
9 + 4 + 2 = 12
15 = 12 pernyataan salah. Jadi, titik (3,1, −2) tidak terletak pada bidang D
d. (4, 1, −4)
3.4 + 4.1 − (−4) = 12
12 + 4 + 4 = 12
20 = 12 pernyataan salah. Jadi, titik (4,1, −4) tidak terletak pada bidang D
Contoh Soal SPLTV 2
Diketahui sistem persamaan:
sumber: tirto.id
Tentukan nilai 𝑎, 𝑏, dan 𝑐 sehingga sistem persamaan tersebut mempunyai penyelesaian!
(−1, 2, −3)
Pembahasan
𝑎𝑥 + 𝑏𝑦 + 𝑐𝑧 = −3 … (1)
𝑏𝑦 + 𝑐𝑧 = 2 … (2)
𝑐𝑧 = −6 … (3)
Penyelesaian sistem persamaan tersebut adalah (−1, 2, −3) maka nilai 𝑥 = −1, 𝑦 = 2 dan 𝑧 =
−3. Sehingga dapat disubstitusikan ke dalam persamaan. Substitusi 𝑧 = −3 ke dalam persamaan (3)
𝑐𝑧 = −6 ⇔ 𝑐(−3) = −6 ⇔ 𝑐 = 2
Substitusi 𝑦 = 2 dan 𝑐𝑧 = −6 ke dalam persamaan (2)
𝑏𝑦 + 𝑐𝑧 = 2
– 𝑏. 2 + (−6) = 2
– 2𝑏 − 6 = 2
– 2𝑏 = 8
– 𝑏 = 4
Substitusi 𝑏𝑦 + 𝑐𝑧 = 2 dan 𝑥 = −1 ke persamaan (1)
𝑎𝑥 + 𝑏𝑦 + 𝑐𝑧 = −3
– 𝑎𝑥 + 𝑏𝑦 + 𝑐𝑧 = −3
– 𝑎𝑥 + 2 = −3
– 𝑎𝑥 = −5
– 𝑎. (−1) = −5
– 𝑎 = 5
Jadi, nilai 𝑎 = 5, 𝑏 = 4 dan 𝑐 = 2
Contoh Soal SPLTV 3
Tentukan penyelesaian SPLTV berikut dengan cara substitusi!
𝑎 + 2𝑏 + 3𝑐 = 8
{2𝑎 + 2𝑏 + 4𝑐 = 10 2𝑎 + 4𝑏 + 2𝑐 = 4
Pembahasan
𝑎 + 2𝑏 + 3𝑐 = 8 . . . (1)
2𝑎 + 2𝑏 + 4𝑐 = 10 ⇔ 𝑎 + 𝑏 + 2𝑐 = 5 . . . (2)
2𝑎 + 4𝑏 + 2𝑐 = 4 ⇔ 𝑎 + 2𝑏 + 𝑐 = 2 . . . (3)
Dari persamaan (1)
𝑎 + 2𝑏 + 3𝑐 = 8
– 𝑎 = 8 − 2𝑏 − 3𝑐 . . . (4)
substitusi persamaan (4) ke dalam persamaan (2)
𝑎 + 𝑏 + 2𝑐 = 5
– (8 − 2𝑏 − 3𝑐) + 𝑏 + 2𝑐 = 5
– −𝑏 − 𝑐 = −3 . . . (5)
substitusi persamaan (4) ke dalam persamaan (3)
𝑎 + 2𝑏 + 𝑐 = 2
– (8 − 2𝑏 − 3𝑐) + 2𝑏 + 𝑐 = 2
– −2𝑐 = − 6
– 𝑐 = 3
substitusi c =3 ke persamaan (5)
−𝑏 − 𝑐 = − 3
– −𝑏 − 3 = −3
– −𝑏 = −3 + 3
– −𝑏 = 0
– 𝑏 = 0
substitusi 𝑏 = 0 dan c = 3 ke persamaan (1)
𝑎 + 2𝑏 + 3𝑐 = 8
– 𝑎 + 2.0 + 3.3 = 8
– 𝑎 + 0 + 9 = 8
– 𝑎 + 9 = 8
– 𝑎 = 8 − 9
– 𝑎 = − 1
Jadi, penyelesaian 𝑎 = −1, 𝑏 = 0 dan 𝑐 = 3
Contoh Soal SPTV 4
Tentukan penyelesaian SPLTV berikut dengan metode substitusi
𝑥 − 𝑦 + 2𝑧 = −5
{2𝑥 + 𝑦 + 𝑧 = −1
𝑥 + 𝑦 − 𝑧 = 3
Pembahasan
𝑥 − 𝑦 + 2𝑧 = −5 … (1)
2𝑥 + 𝑦 + 𝑧 = −1 … (2)
𝑥 + 𝑦 − 𝑧 = 3 … (3)
Isolasi 𝑥 dari persamaan (1), sehingga diperoleh
𝑥 − 𝑦 + 2𝑧 = −5
– 𝑥 = −5 + 𝑦 − 2𝑧 … (4)
Substitusi persamaan (4) ke dalam persamaan (2)
2𝑥 + 𝑦 + 𝑧 = −1
– 2(−5 + 𝑦 − 2𝑧) + 𝑦 + 𝑧 = −1
– −10 + 2𝑦 − 4𝑧 + 𝑦 + 𝑧 = −1
– 3𝑦 − 3𝑧 = 9 … (5)
Substitusi persamaan (4) ke dalam persamaan (3)
𝑥 + 𝑦 − 𝑧 = 3
– (−5 + 𝑦 − 2𝑧) + 𝑦 − 𝑧 = 3
– 2𝑦 − 3𝑧 − 5 = 3
– 2𝑦 − 3𝑧 = 8 … (6)
Isolasi 𝑦 dari persamaan (5), sehingga diperoleh
3𝑦 − 3𝑧 = 9
– 3𝑦 = 9 + 3𝑧
– 𝑦 = 3 + 𝑧 … (7)
Substitusi persamaan (7) ke dalam persamaan (6)
2𝑦 − 3𝑧 = 8
– 2(3 + 𝑧) − 3𝑧 = 8
– 6 + 2𝑧 − 3𝑧 = 8
– −𝑧 = 8 − 2
– 𝑧 = −2
Substitusi 𝑧 = −2 ke dalam persamaan (7)
𝑦 = 3 + 𝑧
– 𝑦 = 3 + (−2)
– 𝑦 = 1
Substitusi 𝑦 = 1 dan 𝑧 = −2 ke dalam persamaan (4)
𝑥 = −5 + 𝑦 − 2𝑧
– 𝑥 = −5 + 1 − 2(−2)
– 𝑥 = −5 + 1 + 4
– 𝑥 = 0
Jadi, penyelesaian 𝑥 = 0, 𝑦 = 1 dan 𝑧 = −2
Contoh Soal SPTV 5
Tentukan penyelesaian SPLTV berikut dengan metode substitusi
4𝑥 − 3𝑦 + 𝑧 = 19
{3𝑥 − 2𝑦 − 2𝑧 = 16
𝑥 + 5𝑦 + 7𝑧 = −25
Pembahasan
4𝑥 − 3𝑦 + 𝑧 = 19 … (1)
3𝑥 − 2𝑦 − 2𝑧 = 16 … (2)
𝑥 + 5𝑦 + 7𝑧 = −25 … (3)
Isolasi 𝑧 dari persamaan (1), sehingga diperoleh
4𝑥 − 3𝑦 + 𝑧 = 19
– 𝑧 = 19 − 4𝑥 + 3𝑦 … (4)
Substitusi persamaan (4) ke dalam persamaan (2)
3𝑥 − 2𝑦 − 2𝑧 = 16
– 3𝑥 − 2𝑦 − 2(19 − 4𝑥 + 3𝑦) = 16
– 3𝑥 − 2𝑦 − 38 + 8𝑥 − 6𝑦 = 16
– 11𝑥 − 8𝑦 = 54 …. (5)
Substitusi persamaan (4) ke dalam persamaan (3)
𝑥 + 5𝑦 + 7𝑧 = −25
– 𝑥 + 5𝑦 + 7(19 − 4𝑥 + 3𝑦) = −25
– 𝑥 + 5𝑦 + 133 − 28𝑥 + 21𝑦 = −25
– −27𝑥 + 26𝑦 = −158 … (6)
Isolasi 𝑦 dari persamaan (5)
sumber: tirto.id
sumber: tirto.id
– 𝑧 = 19 − 4𝑥 + 3𝑦
– 𝑧 = 19 − 4.2 + 3(−4)
– 𝑧 = 19 − 8 − 12
– 𝑦 = −1
Jadi, penyelesaian 𝑥 = 2, 𝑦 = −4 dan 𝑧 = −1
***
Semoga bahasan contoh soal SPLTV ini bisa bermanfaat untuk kamu ya, Property People.
Jangan lupa untuk membaca ulasan menarik lainnya, seperti contoh soal peluang hanya di Berita.99.co.
Yuk, follow Google News kami untuk mendapatkan berbagai informasi paling up to date.
Kunjungi pula laman www.99.co/id guna menemukan beragam rumah idaman dan properti lainnya.
Dapatkan berbagai promo dan diskon menggiurkan karena ternyata beli hunian emang #segampangitu, lo.
